
关于分割问题,存在多种情况,在此进行汇总,对问题进行分析,对所用到的公式进行推导。
1.直线分割
题目:n 个点最多可以把一条直线划分成多少段
公式:A(n) = n+1
2.平面分割
题目:n 条直线,最多可以把平面分为多少个区域。
公式:B(n) = n(n+1)/2+1
分析:
假设平面上已有 n 条直线它们把平面划分成最多的区域,那么第 n+1 条直线下去的时候,为了保证获得最多的区域,那么要求这条直线和之前的 n 条直线都相交,并且新产生的交点不和之前的交点重合.显然第 n+1 条直线和之前的 n 条直线产生 n 个交点,这 n 个交点把第 n+1 条直线划分成 A(n)段,每一段都将原来的区域一分为二,于是 B(n+1)=B(n)+A(n)。
推导:
A(n) = n+1
B(1) = 2
B(n)= B(n-1)+ A(n-1)
= B(n-2) + n + n-1
= n+....+2+B(1)
= n+...+2+1+1
= n(n+1)/2 + 1
3.空间分割
题目:n 条直线,最多可以把平面分为多少个区域。
公式:C(n) = (n^3+5n)/6+1
分析:
第 n+1 个平面下去多增加了多少块,前面的 n 个平面都和第 n+1 个平面相交,在第 n+1 个平面上留下 n 条交线,这 n 条交线最多将第 n+1 个平面划分成 B(n)个区域,每个区域都将原来的块一分为二,于是 C(n+1)=C(n)+B(n)。
推导:
B(1) = 2
C(1) = 2
C(n)= B(n-1)+C(n-1)
= n(n-1)/2+1 + (n-1)(n-2)/2+1 + C(n-2)
= n(n-1)/2+.....+3+1 + 2+ (n-1)
=(1*2+2*3+....+n*(n-1))/2 + n+1
=(1+2^2+3^2+4^2+....+n^2 - (1+2+3+...+n))/2 + n+1
=(n(n+1)(2n+1)/6-n(n+1)/2) + n+1
= (n^3-n)/6 + n+1
= (n^3+5n)/6+1
实例:
小Py要吃西瓜,想知道切了n刀后,最多能切出多少块?请你们帮助下小Py.
给你一个正整数n(0 < n < 10^3),你输出一个数字,代表最多能切多少块。
如n=1, 输出2。
4.折线分割平面
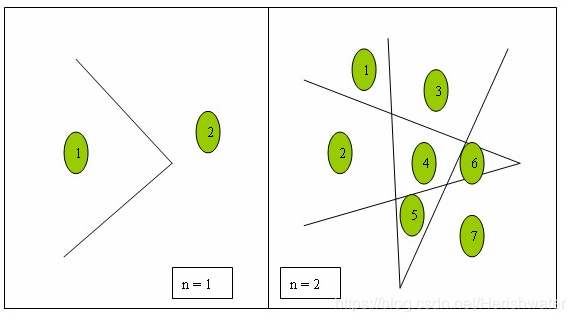
公式:D(n) = 2n^2-n+1
分析:
根据直线分平面可知,增加第 n 条直线的时候,跟之前的直线最多有 n-1 个交点,此时分出的部分多出了(n-1)+1。由交点决定了射线和线段的条数,进而决定了新增的区域数。D(1) = 2,D(2) = 7,当n-1条折线时,区域数为 D(n-1)。为了使增加的区域最多,则折线的两边的线段要和 n-1 条折线的边,即 2*(n-1)条线段相交。所以分出的部分多出了 2*2(n-1)+1,所以推出D(n)=D(n-1)+4*(n-1)+1,n>=3。
推导:
D(1) = 2
D(2) = 7
D(n)= D(n-1)+4(n-1)+1
= 4(n-2)+4(n-1) +D(n-2) +1
=4(n-1+n-2+...+1)+D(1) + n-1
=4(n(n-1)/2) + 1+n
2n^2-n+1
5.封闭曲线切割平面
题目:设有n条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,
问这些封闭曲线把平面分割成的区域个数。
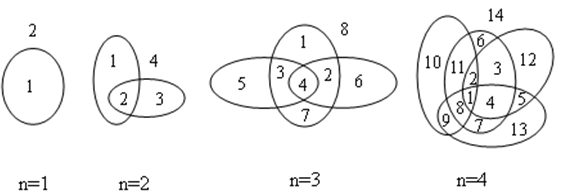
公式:F(n) = n^2-n+2
分析:
当 n-1 个圆时,区域数为 F(n-1).那么第 n 个圆就必须与前 n-1 个圆相交,则第 n 个圆被分为 2(n-1)段线段,增加了 2(n-1)个区域。
推导:
F(1) = 2
F(n)= F(n-1) + 2(n-1)
= 2(n-1+n-2+....+1) + F(1)
=n^2-n+2
本文作者为hresh,转载请注明。