
前言
佩尔方程是一种不定二次方程。
下面的不定方程称为佩尔(Pell)方程:
其中 d 为正整数,若 d 是完全平方数,则这个方程式只有平凡解(1,-1,0)。若 d 是非平方数。佩尔方程存在无穷多个解。
若佩尔方程的最小特解(最小正整数解)是(x1,y1),那么可有迭代公式:
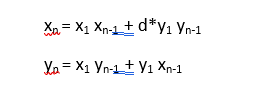
除了上述常见的佩尔方程,还有一种形式。下面的不定方程称为第II型佩尔(Pell)方程:
如果②有正整数解,设(a,b)是②的正整数解中使 x+y√d 最小的解(称(a,b)为②的基本解),则②的全部正整数解可以表示为:
x+y√d=(a+b√d)^(2n+1) (n为任意正整数)
而且记x0+y0√d=(a+b√d)^2,则(x0,y0)为①的基本解。
关于公式②的通解,可以前往阅读数论笔记 · 佩尔方程,该文章对此进行了详细讲解。这里我们就直接拿来使用。

如上图所示,当 K 为 -1 时,即和公式②一致,此时 p,q 为公式②的解,(r,s)为公式①的基本解。将公式①和公式②进行相乘,最终得到(x,y)的通解。假设 D 为 2,公式①的基本解为(3,2),则(x,y) = (3p±4q,2p±3q)。
实例分析
案例一
记得有一次全班去唱K, 其中有个活动是情歌对唱. 具体操作流程是这样的:
准备好 21 个阄(我们班 15 男 6 女), 其中只有两个是有标记的, 每人随意抓取一个, 最后取到有标记的阄的两个人去点首情歌对唱.
旁边一哥们儿幽幽地对我说, 看来搅基真是神的安排啊, 你看我们班的男女人数, 搅基的几率 C(15,2)/C(21,2) 刚好是 1/2.
给跪了, 这哥们儿对数字太敏感了, 简直是拉马努金转世啊. 不过我随之想到一个问题: (21, 15) 真的是神的唯一安排吗? 其实不是的,
神还有很多类似的安排. 比如 (4, 3), 显然 C(4,2)/C(3,2) 也等于 1/2, 当然还有 (120, 85) 等等等等.
神的安排太多太多了, 如果我们定义 (n, m) 是一个安排(其中 1 < m < n), 而如果 C(m,2)/C(n,2) = 1/2, 它就是神的安排.
现在的问题是, 给你一个不大于 10^9 的正整数 N, 有多少组神的安排 (n, m) 满足 n <= N 呢?
分析:
根据题意列出方程 2*m^2-2*m=n^2-n,转换为佩尔方程形式:(2*n-1)^2-2*(2*m-1)^2=-1。
记 x = 2n-1,y=2m-1,原方程即为:x^2-2*y^2=-1。为了求解该方程的通解,需要先计算x^2-2*y^2=1的基本解,显然(3,2)为基本解,套用上述得到的通解公式,可以得到 xn,yn 的迭代公式:
x(n+1) = 3xn±4yn
y(n+1) = 2xn±3yn
#由于题目解要求为正整数且 x(n+1) 大于 xn,(1,1)为方程基本解,因此选择乘积相加,而非相减。
x(n+1) = 3xn+4yn
y(n+1) = 2xn+3yn
代码实现:
N = 54
def cal_probability2():
global N
x = 1
y = 1
n = 0
xy_list = []
while (x + 1) / 2 <= N:
a = x
b = y
if x>y:
xy_list.append(((x + 1) // 2, (y + 1) // 2))
n += 1
x = 3 * a + 4 * b
y = 2 * a + 3 * b
print(n)
print(xy_list)
输出结果为:
2
[(4, 3), (21, 15)]
案例二
数1,3,6,10,....构成数列{a_n},数1,4,9,16,....构成数列{b_n}。将既是数列{a_n}中的项,又是数列{b_n}中的项按照从小到大的顺序
构成新的数列{c_n},试写出数列{c_n}的前4项。
分析:
数列{a_n}的通项公式是 a_n = n(n+1)/2,数列{b_n}的通项公式是 b_n = n^2。要找出两个数列中的公共项,可以让两个通项公式相等。此时,令 a_n = b_m,即 n(n+1)/2 = m**2,因为不确定 m 和 n 是否完全相同,因此分开来区别表示。
由 n(n+1)/2 = m2 可得 (2n+1)2-8*m^2 = 1,令 x = 2n+1,y = m,则方程变为:x^2 - 8*y^2 = 1,其中(3,1)为该方程的基本解。
代码实现:
N = 4
n = 1
a = 3 #方程最小解(x1,y1)
b = 1
nm_list = []
while n<=4:
x = a
y = b
nm_list.append(((x-1)//2,y))
a = 3*x+8*y
b = x+y*3
n += 1
print(nm_list)
result = []
for w in nm_list:
b_n = w[1]**2
result.append(b_n)
print(result)
输出结果为:
[(1, 1), (8, 6), (49, 35), (288, 204)]
[1, 36, 1225, 41616]
后续会继续更新相关知识点。
本文作者为hresh,转载请注明。