Python 判断两个单链表的交点

前言

在前面两章有介绍过单链表的基本操作以及有环链表的相关问题。本章主要分析两个单链表的交点问题。

首先声明，两个单链表只能存在 Y 型交叉，不会存在 X 型交叉。因为如果是 X 型交叉，节点在交叉点之后便不知道 next 指针指向为哪一个节点。

实战分析

判断单链表是否相交存在三种情况：

1. 两个单链表都没有环。
2. 两个单链表中 一个有环，一个没有环。
3. 两个链表都有环。

情况 1

对于仅判断相交不相交的话：判断最后一个节点是否相同的办法并不慢，如果两个链表长度m,n 那么复杂度O(m+n)，这是最优的复杂度。

def judge_list_equals(a:SingleLinkList, b:SingleLinkList):
    '''
    判断两个单链表是否相交，复杂度为两个链表长度之和
    :param a: 单链表a
    :param b: 单链表b
    :return:
    '''
    p = a.get_header()
    q = b.get_header()

    while p != None :
        p = p.next

    while q != None:
        q = q.next

    if p == q:
        return True
    return False

寻找交叉点。遍历两个表分别知道两个表的长度 a, b。然后让长表先走|a-b|步后，短表再开始走，直到相同，即为交叉点。（注明：本章求解的交叉点均为第一个相交点，第一个相交点是以相对单链表的开头来说，顺序行走后的某个节点）

def get_intersection(a:SingleLinkList, b:SingleLinkList):
    '''
    计算两个单链表的交叉点
    :param a:
    :param b:
    :return:
    '''
    a_size = a.size()
    b_size = b.size()

    s_max_link = a if a_size >= b_size else b
    s_min_link = a if a_size < b_size else b

    size_diff = abs(a_size-b_size)

    p = s_max_link.get_header()
    for i in range(size_diff):
        p = p.next

    q = s_min_link.get_header()

    print(p,q)

    while p != None and q != None:
        p = p.next
        q = q.next
        if p == q:
            return p
    return None

需要更新 Node 对象。

class Node():
    def __init__(self, val=None):
        self.val = val  #节点数据值
        self.next = None    #相连的下一个节点对象

    def __str__(self):
        return str(self.val)

    def __eq__(self, other):
        if other == None:
            return False
        return self.val == other.val

情况 2

当一个链表有环，另一个链表无环，那么两个链表肯定不相交。

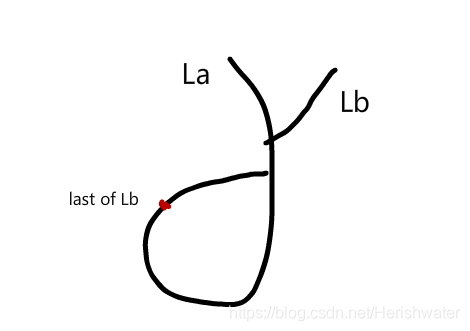
如上图所示，假设链表 La 有环，Lb 无环，交点在 La 环点之前。那么问题来了，Lb 的尾节点应该在哪里，不管是在 La 的入环点之前还是 La 的环上，都是有问题的。正如链表的设计理念一样，每个节点只能有一个指向下个节点的指针，Lb 的尾节点指向 None，但是 La 在 Lb 尾节点处还要指向下一个非 None 节点，而这种情况又不存在，所以情况 2 判断链表是不会相交的。

情况 3

当两个链表都为有环链表时，关于链表的交点的位置存在以下三种可能。

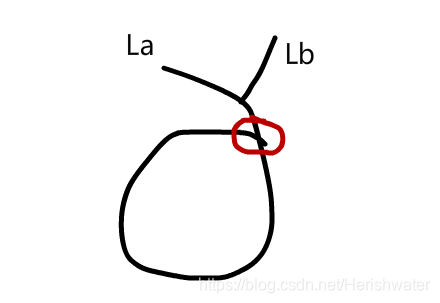
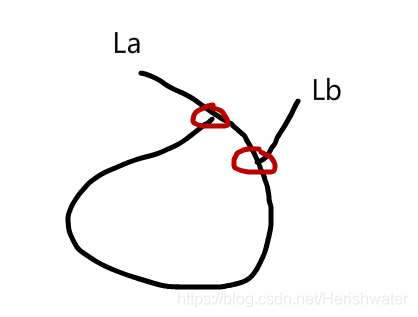
关于有环链表求解入环点，在上一章中详细讲解过。

其实 a 情况和 b 情况又类似，因为它们相交之后，后面的节点都是一样的，所以还是可以采用情况 1 中的解析方法。

def get_intersection(a:SingleLinkList, b:SingleLinkList, a_size:int, b_size:int):
    '''
    计算两个单链表的交叉点
    :param a:
    :param b:
    :return:
    '''
    # a_size = a.size()
    # b_size = b.size()

    s_max_link = a if a_size >= b_size else b
    s_min_link = a if a_size < b_size else b

    size_diff = abs(a_size-b_size)

    p = s_max_link.get_header()
    for i in range(size_diff):
        p = p.next

    q = s_min_link.get_header()

    while p != None and q != None:
        p = p.next
        q = q.next
        if p == q:
            return p
    return None

if __name__ == '__main__':
    sa = SingleLinkList()
    sb = SingleLinkList()

    sa.add('a1')
    sa.add('a2')
    sa.add('c1')
    sa.add('c2')
    sa.add('c3')
    sa.add('c4')

    sb.add('b1')
    sb.add('b2')
    sb.add('b3')
    sb.add('c1')
    sb.add('c2')
    sb.add('c3')
    sb.add('c4')

    a_size = sa.size()
    b_size = sb.size()
    sa.setCycleList(3)
    sb.setCycleList(4)

    print(get_intersection(sa,sb,a_size,b_size))

首先将单链表转换为有环链表，记录转换前的链表长度，用于后续使用。

c 情况与前面两种情况不一样，交点之后的节点走的顺序队列是不同的，这就导致存在两个交点，如图所示：

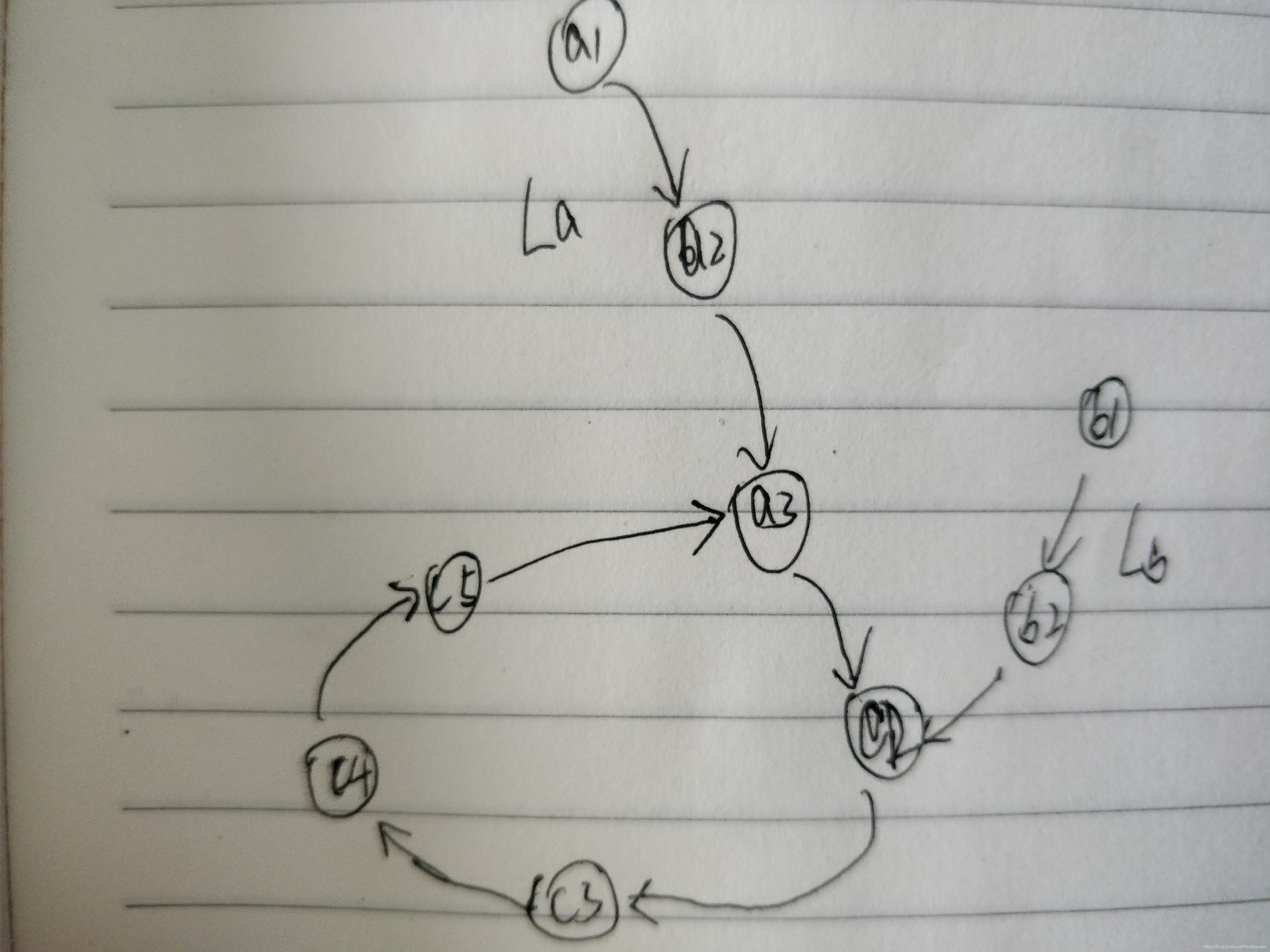
在 a3 节点处相交后，节点走序为：c2-c3-c4-c5-a3-c2.......；在 c2 节点处相交后，节点走序为：c3-c4-c5-a3-c2-c3......

两个链表的环上的节点序列是一致的，只是各自的入环点不一致，关于交点可以这么理解：相对于 La（入环点为 a3）来说它和 Lb 的交叉点即为自身的入环点，而对于 Lb（入口点为 c2）来说它与 La 的交叉点为 c2。因此，当两个有环链表相交时，存在两个交叉点，分别为各自的入环点（关于有环链表的入环点求解可以借鉴上一章的讲解内容）。

同时声明，c 情况是根据自己的理解进行分析的，如果有错误之处，还望指出，我会尽快改正。