Python 实现二叉搜索树（BST）

前言

二叉搜索树（Binary Search Tree）是一种特殊的二叉树，支持多种动态集合操作，如 Search、Insert、Delete、Minimum 和 Maximum 等。

二叉查找树要么是一棵空树，要么是一棵具有如下性质的非空二叉树：

• 若左子树非空，则左子树上的所有节点的关键字值均小于根节点的关键字值。
• 若右子树非空，则右子树上的所有节点的关键字值均大于根节点的关键字值。
• 左、右子树本身也分别是一棵二叉查找树（二叉排序树）。

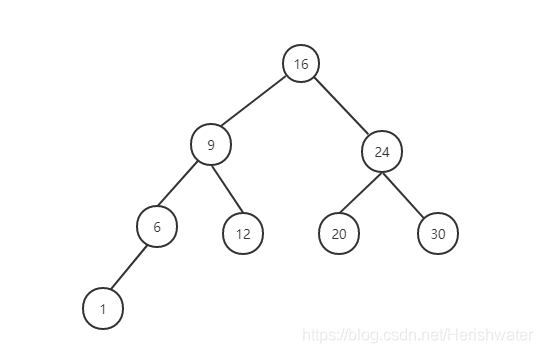
可以看出，二叉搜索树中各个节点都不相同，且对二叉查找树进行中序遍历，可以得到一个递增的有序序列。如图所示，构建二叉搜索树时，需要注意节点元素的大小。

实战分析

首先，我们来定义一下 BST 的节点对象，结点中除了 val 域，还包含域 left, right 和 parent，它们分别指向节点的左儿子、右儿子和父节点：

class TreeNode():
    def __init__(self, x=None):
        self.val = x
        self.left = None
        self.right = None
        self.parent = None

    def __str__(self):
        return str(self.val)

一、BST 的构造与插入

二叉搜索树作为一种动态结构，其特点是树的结构通常不是一次生成的，每次插入都需要判断树中是否存在该节点，若无则允许插入。

由于二叉查找树是递归定义的，插入节点的过程是：若原二叉查找树为空，则直接插入；否则，若关键字 k 小于根节点关键字，则插入到左子树中，若关键字 k 大于根节点关键字，则插入到右子树中。

class BST():
    def __init__(self, node=None):
        '''
        设置根节点
        :param node: 根节点
        '''
        node = TreeNode(node)
        self.root_node = node

    def insert(self, x):
        '''
        二叉树做插入操作
        :param x:
        :return:
        '''
        if self.is_exist(x):#判断树中是否存在该节点
            return
        p = TreeNode(x)
        if self.root_node == None:#如果树为空的话，则将插入的节点置为根节点
            self.root_node = p
        else:
            cur = self.root_node
            pre = None
            while cur != None:#利用非递归的方法遍历
                pre = cur
                if cur.val < x:
                    cur = cur.right
                else:
                    cur = cur.left

            p.parent = pre
            if pre.val < x:
                pre.right = p
            else:
                pre.left = p

    def is_exist(self, k):
        '''
        判断二叉树中是否存在某节点的数值与 k 相等
        :param k:
        :return:
        '''
        cur = self.root_node
        while cur != None and cur.val != k:
            if k < cur.val:
                cur = cur.left
            else:
                cur = cur.right
        return True if cur != None else False

if __name__ == '__main__':
    bs_tree = BST(16)   #初始化二叉树
    #对二叉树做插入操作
    bs_tree.insert(9)
    bs_tree.insert(24)
    bs_tree.insert(12)
    bs_tree.insert(6)
    bs_tree.insert(20)
    bs_tree.insert(30)

具体过程是：每读入一个元素，就建立一个新节点；若二叉查找树为空，则新节点作为根节点；若二叉查找树非空，则将新节点的值与根节点的值比较，如果小于根节点的值，则插入到左子树中，否则插入到右子树中。

注意，插入的新节点一定是某个叶子节点。另外，插入操作既可以递归实现，也可以使用非递归（迭代）实现。通常来说非递归的效率会更高。因此本程序中采用的是非递归方式。

二、BST 的遍历

二叉搜索树的性质允许通过简单的递归算法来输出树中所有的关键字，有三种方式：先序遍历（根左右）、中序遍历（左根右）、后序遍历（左右根）。

如果 x 是一棵有 n 个节点子树的根，那么不管是那种遍历方式都需要O(n)时间。

1.先序遍历

    def preorder_tree_walk(self, n):
        '''
        先序遍历树节点（根左右）
        :param n:
        :return:
        '''
        if n != None:
           print(n.val, end=' ')
           self.preorder_tree_walk(n.left)
           self.preorder_tree_walk(n.right)

2.中序遍历

    def inorder_tree_walk(self, n):
        '''
        中序遍历树节点（左根右）,输出结果正好是排序好的顺序
        :param n:
        :return:
        '''
        if n != None:
            self.inorder_tree_walk(n.left)
            print(n.val, end=" ")
            self.inorder_tree_walk(n.right)

对于中序遍历，用图解的形式展示出来：

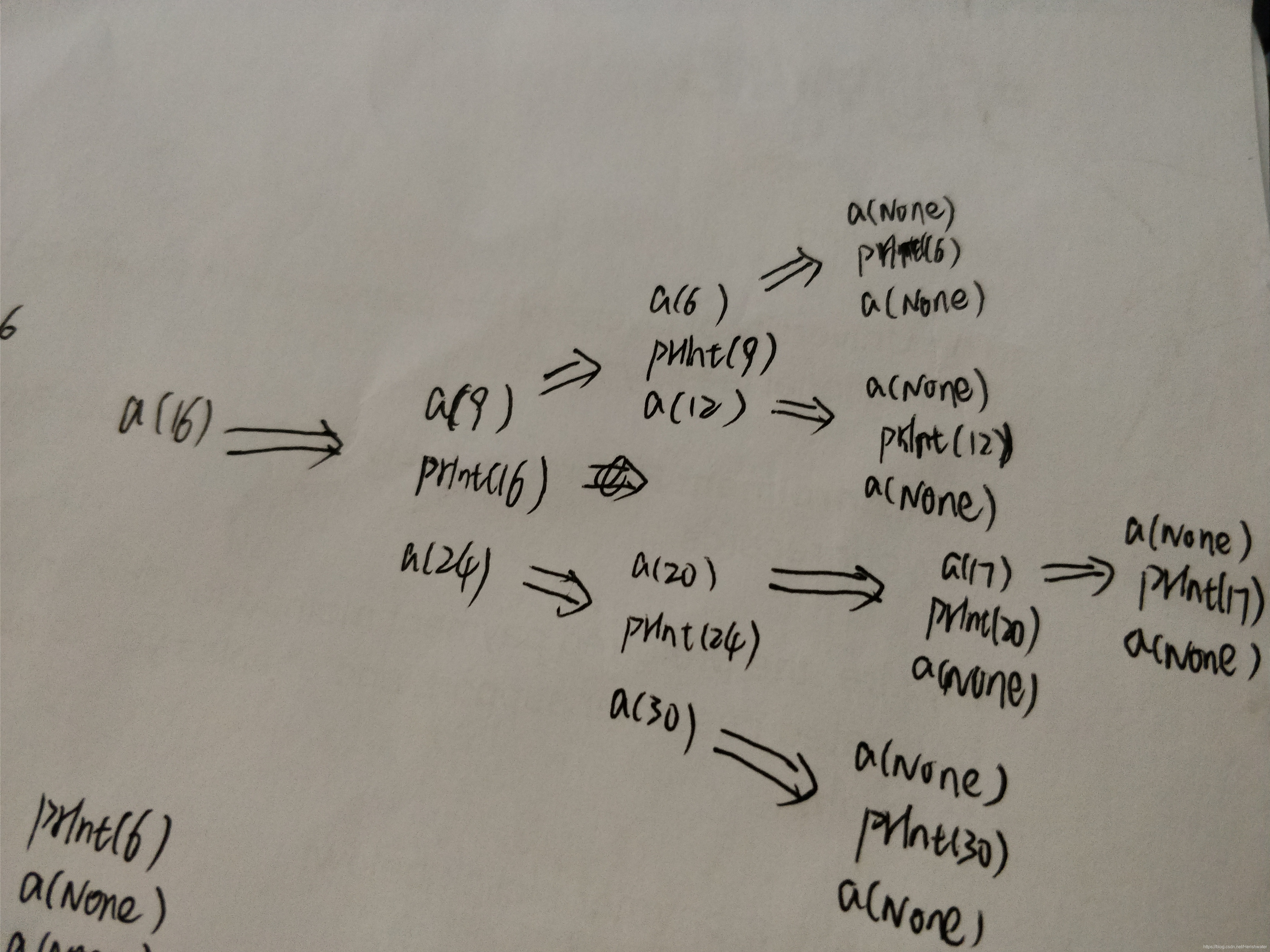
需要注意的是：在后续查找二叉搜索树中第 k 大节点值的时候，当 count 值已经等于 k 时，假设想要输出 17，程序print(n.val, count,k,flag)还是输出 20 和 24，皆因为输出 17 后回退过程中输出了 20 和 24，但是并不会继续查找节点 24 的右子树。

3.后序遍历

    def postorder_tree_walk(self, n):
        '''
        后序遍历树节点（左右根）
        :param n:
        :return:
        '''
        if n != None:
            self.postorder_tree_walk(n.left)
            self.postorder_tree_walk(n.right)
            print(n.val, end=' ')

其中中序遍历输出的结果顺序和排序后的顺序一致，后续会使用到中序遍历。

三、BST 的查找

对于二叉搜索树，最常见的操作就是查找树中的某个关键字。由于二叉搜索树中序排列的时候是个有序序列，所以我们还可以查找第 k 大的节点，以及查找某节点左子树上的最大节点和右子树上的最小节点。

1.查找

    def find_node(self, k):
        '''
        找到值为k的节点并返回
        :param k:
        :return:
        '''
        cur = self.root_node
        while cur != None and cur.val != k:
            if k < cur.val:
                cur = cur.left
            else:
                cur = cur.right
        return cur

BST 的查找是从根节点开始，若二叉树非空，将给定值与根节点的关键字比较，若相等，则查找成功；若不等，则当给定值小于根节点关键字时，在根节点的左子树中查找，否则在根节点的右子树中查找。采用非递归的方式求解。

2.查找第 k 大值

    def search(self, k):
        '''
        二叉搜索树按照中序遍历的顺序打印出来正好就是排序好的顺序
        从二叉树中查找第k大的节点元素
        :param k:
        :return:
        '''
        count = 0
        val = None
        flag = False

        def inorder(n):
            nonlocal count,val,flag

            # if flag:
            #     return

            if n != None:
                inorder(n.left)
                count += 1
                print(n.val, count,k,flag)
                if count == k:
                    val = n.val
                    flag = True
                    n.left = None
                    n.right = None
                if count > k:
                    return

                inorder(n.right)

        inorder(self.root_node)
        return val

采用中序遍历的方式进行计数，与 k 值相比较。

3.节点左子树最大值

    def find_max_node(self, node):
        '''
        查找node节点左子树中最大的那个节点，按照中序遍历（左根右）的顺序可知，左子树最大的那个节点通过判断node.right不断往下查找
        :param node:
        :return:
        '''
        np = TreeNode()
        np = node

        if np == None:
            return None
        while np.right != None:
            np = np.right
        return np

4.节点右子树最小值

    def find_min_node(self, node):
        '''
        查找node右子树上最小的节点
        :param node:
        :return:
        '''
        np = TreeNode()
        np = node

        if np == None:
            return None
        while np.left != None:
            np = np.left
        return np

四、BST 的删除

二叉查找树的删除操作是相对复杂一点，它要按 3 种情况来处理：

• 若被删除节点 z 是叶子节点，则直接删除，修改 z 的父节点的指向，不会破坏二叉搜索树的性质；
• 若节点 z 的后继 x （如果有右子树，则提取的是右子树中的最小值，否则提取的是左子树中的最大值）， z 是 x 的父节点，则让 x 代替 z 的位置；
• 若节点 z 的后继 x （如果有右子树，则提取的是右子树中的最小值，否则提取的是左子树中的最大值）， z 与 x 不直接相连，则先删除节点 z，把 x 放在 z 的位置，同样还要考虑 x 的后继 x1 ，这样递归下去，直到转换成第一或第二种情况。

情况 1：

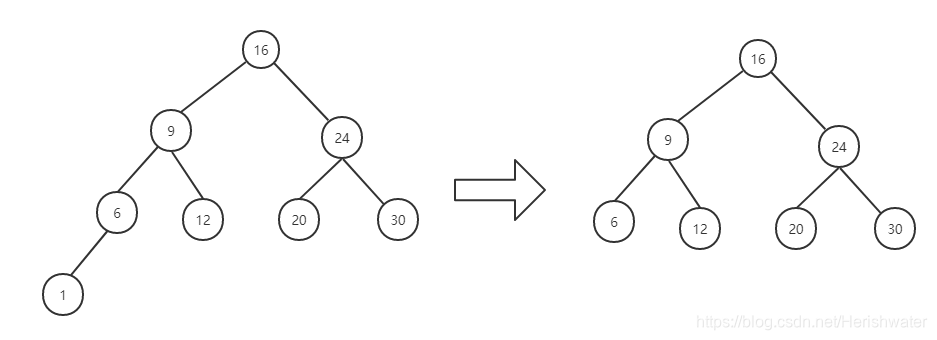
情况 2：

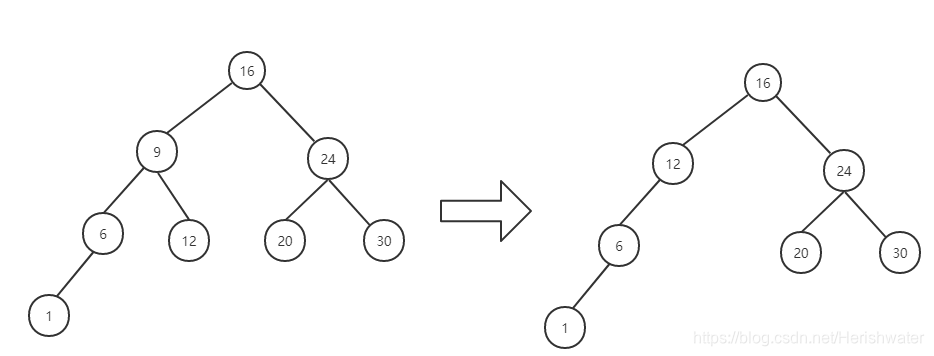
情况 3：

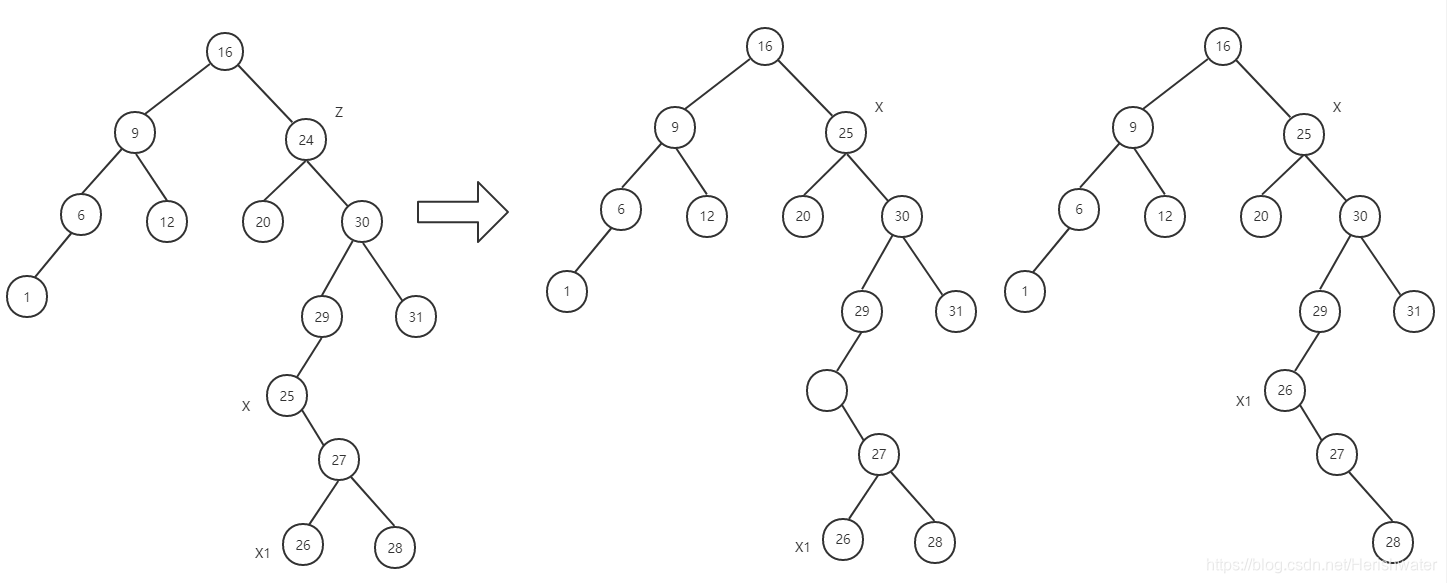
代码实现：

    def delete_leaf(self, node):
        cur_parent = node.parent
        if cur_parent != None:
            if node.val < cur_parent.val:
                cur_parent.left = None
            else:
                cur_parent.right = None
        else:
            self.root_node = None

        def delete(self, node):

        if self.is_leaf(node):#为叶子节点时，直接删除
            self.delete_leaf(node)
        else:
            replace_node = self.find_min_node(node.right) if node.right != None else self.find_max_node(node.left)
            # replace_node = self.find_max_node(node.left) if node.left != None else self.find_min_node(node.right)

            rep_node = TreeNode()
            rep_node = copy.copy(replace_node)#浅复制，保持原有的节点指向

            if node == replace_node.parent:#如果后继和node相关联，则按照以下方法处理
                if node.val < node.parent.val:
                    node.parent.left = replace_node
                else:
                    node.parent.right = replace_node
                replace_node.parent = node.parent
                if replace_node != node.left:
                    replace_node.left = node.left
                    node.left.parent = replace_node
            else:#删除 node 节点后，更新后继节点的父节点和左节点和右节点
                nd_parent = node.parent

                if nd_parent != None:
                    if node.val > nd_parent.val:
                        nd_parent.right = replace_node
                    else:
                        nd_parent.left = replace_node
                else:
                    self.root_node = replace_node
                replace_node.parent = nd_parent

                replace_node.left = node.left
                replace_node.right = node.right

                if node.left != None:
                    node.left.parent = replace_node
                if node.right != None:
                    node.right.parent = replace_node
                # print(rep_node)

                self.delete(rep_node)

这里关于节点 z 的后继，首选是从右子树中查找，只是个人习惯，从左子树中查找也不违背二叉搜索树的定义。

关于二叉搜索树节点的删除，如有错误，请指正。